29. Spatially variable genes

29.1. Motivation

One main analysis step for single-cell data is to identify highly-variable genes (HVGs) and perform feature selection to reduce the dimensionality of the dataset. HVGs are genes which show significantly different expression profiles between cells or distinct groups. Methods designed for this task, however, neglect the spatial context of cells and can therefore not identify spatial variation. A gene might for example be highly variable, but not show a distinct spatial pattern and is therefore not spatially variable.

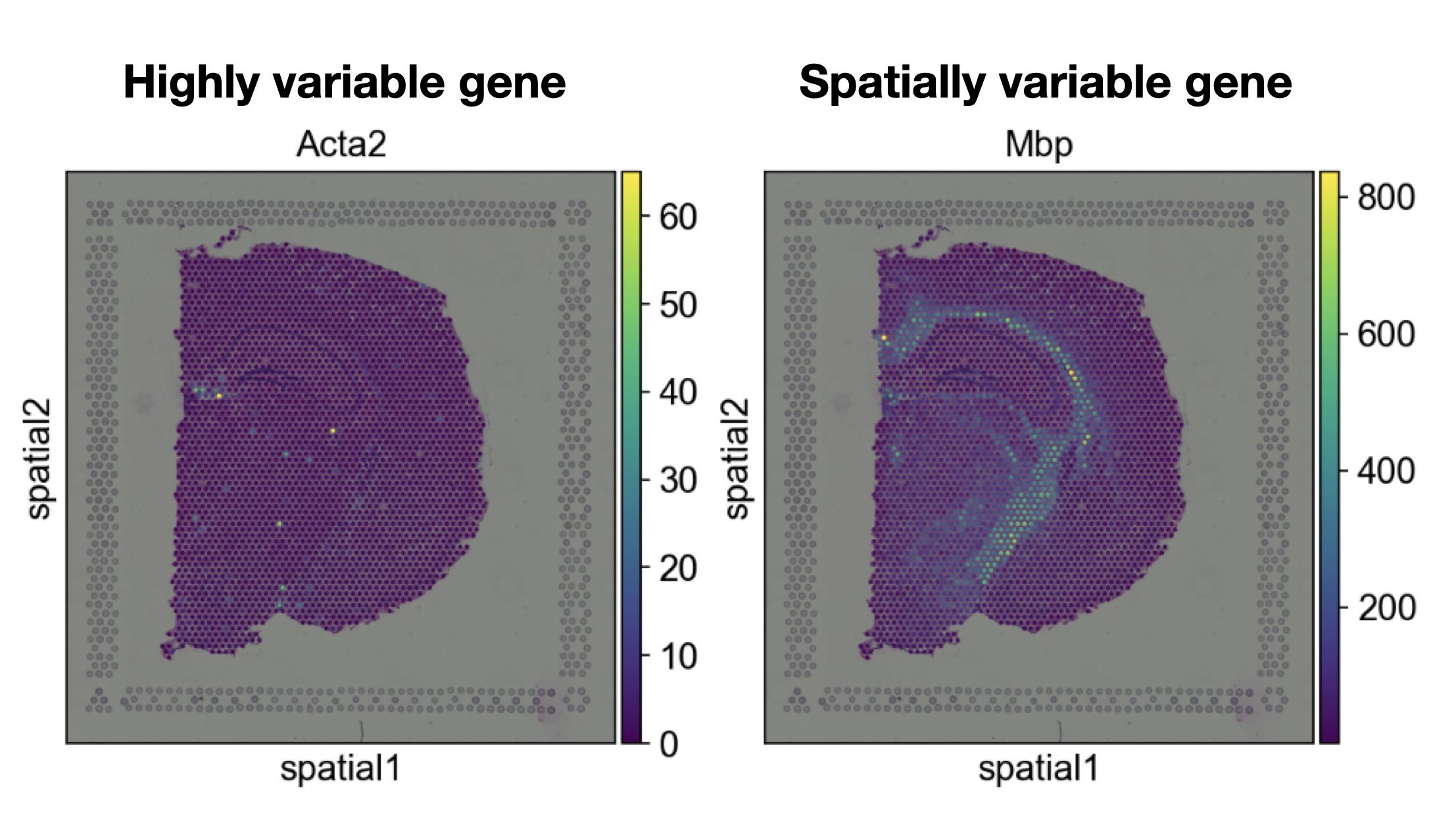
Fig. 29.1 Spatially variable genes are genes that show a distinct spatial pattern, whereas highly variable genes reflect genes that differ significantly between cells or groups of cells.

Spatial variation can be caused by differences in cell-type composition, overall functional dependencies or cell-cell communication events and help to understand the underlying tissue biology. Methods designed to identify spatially variable genes (SVGs) are designed to quantify whether a gene shows a significant spatial pattern by typically decomposing spatial and non-spatial variation in the dataset [Walker et al., 2022].

Several methods have been proposed for this task with varying complexity and different assumptions. Currently there is no consensus on which method works best and how to define spatial variability in general. SpatialDE [Svensson et al., 2018], SpatialDE2 [Kats et al., 2021] and SPARK[Zhu et al., 2021] [Sun et al., 2020] use spatial correlation testing, Sepal[Andersson and Lundeberg, 2021] leverages a Gaussian diffusion on spatial expression, scGCO[Zhang et al., 2022] utilizes a graph cut method and SpaGCN [Hu et al., 2021] identifies SVGs based on spatial domains identified through a graph convolutional neural network.

In this notebook we provide a pedagogical example using Squidpy [Palla et al., 2022] and its implementation of Morans’I to find SVGs and subsequently an example workflow for SpatialDE.

29.2. Environment setup and data

We first load the respective packages needed in this tutorial and the dataset.

import scanpy as sc
import squidpy as sq
import NaiveDE
import SpatialDE

sc.settings.verbosity = 3
sc.settings.set_figure_params(dpi=80, facecolor="white")

The dataset used in this tutorial consists of 1 tissue slides from 1 mouse and is provided by 10x Genomics Space Ranger 1.1.0. The dataset was pre-processed in Squidpy, which provides a loading function for this dataset.

adata = sq.datasets.visium_hne_adata()

29.3. Moran’s I score in Squidpy

One approach for the identification of spatially variable genes is the Moran’s I score, a measure of spatial autocorrelation (correlation of signal, such as gene expression, in observations close in space).

It is defined as: \(I = \frac{n}{W}\frac{{\mathop {\sum }\nolimits_{i = 1}^n \mathop {\sum }\nolimits_{j = 1}^n w_{i,j}z_iz_j}}{{\mathop {\sum }\nolimits_{i = 1}^n z_i^2}}\) where

• \(z_{i}\) is the deviation of the feature from the mean \(\left( {x_i - \bar X} \right)\)

• \(w_{i,j}\) is the spatial weight between observations

• \(n\) is the number of spatial units

• \(W\) is the sum of all \(w_{i,j}\)

It can be computed with Squidpy with 1 line. For the purpose of the example, we will compute it only for a few genes.

sq.gr.spatial_neighbors(adata)
sq.gr.spatial_autocorr(adata, mode="moran", genes=adata.var_names)

Creating graph using `grid` coordinates and `None` transform and `1` libraries.
Adding `adata.obsp['spatial_connectivities']`
       `adata.obsp['spatial_distances']`
       `adata.uns['spatial_neighbors']`
Finish (0:00:00)
Calculating moran's statistic for `None` permutations using `1` core(s)
Adding `adata.uns['moranI']`
Finish (0:00:00)

The method adds a dataframe to adata.uns under the key moranI. We can inspect the result now:

adata.uns["moranI"].head()

	I	pval_norm	var_norm	pval_norm_fdr_bh
Nrgn	0.874753	0.0	0.000131	0.0
Mbp	0.868723	0.0	0.000131	0.0
Camk2n1	0.866542	0.0	0.000131	0.0
Slc17a7	0.861761	0.0	0.000131	0.0
Ttr	0.841986	0.0	0.000131	0.0

The Squidpy implementation of Moran’s I computed for every gene

• I so the Moran’s I,

• pval_norm a p-value under normality assumption.

• var_norm the variance of the Moran’s I under normality assumption.

• {p_val}_{corr_method} the corrected p-values.

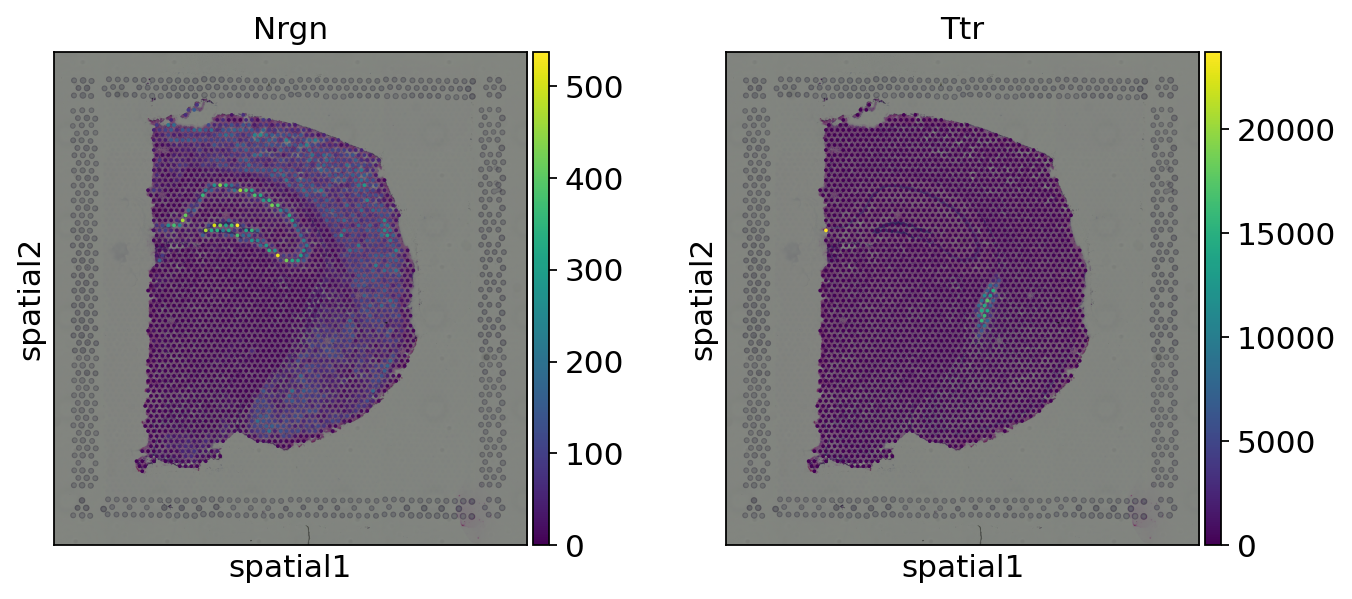
Let us look at two of the identified and significant genes, for example Nrgn and Ttr with corrected p-values of 0.0.

sq.pl.spatial_scatter(adata, color=["Nrgn", "Ttr"])

We can see that the expression of both of these genes seems to show a distinct localization in the tissue. It should be noted that they might (or might not) be also marker genes for specific cell clusters. One interpretation of spatially variable genes identification is that it is an orthogonal way to perform feature selection, by selecting genes that show a variability in space (instead of, for instance, across observations, as it is usually done).

29.4. SpatialDE

SpatialDE identifies spatial variable genes through Gaussian process regression. The spatial method decomposes each gene’s expression variability into a spatial and nonspatial component. It then computes the ratio between the spatial and nonspatial variance term to quantify the overall spatial variance present in the dataset. In order to identify significant spatially variable genes, SpatialDE compares the full model that has access to the spatial component to a model without this term.

We are using the same dataset as we did for computing Moran’s I. As SpatialDE requires the counts table saved as a DataFrame with unique variable names, we first make all variable names unique with the help of the respective Scanpy function.

adata.var_names_make_unique()

Next, we collect the raw count table with all barcode names and variable names saved as dataframe indexes and columns. Scanpy provides an efficient function for this, get.obs_df which collects the respective keys stored in adata.

counts = sc.get.obs_df(adata, keys=list(adata.var_names), use_raw=True)

SpatialDE additionally requires the total counts and the spatial coordinates in the form of a DataFrame. We can use the same Scanpy function of collecting these items as before.

total_counts = sc.get.obs_df(adata, keys=["total_counts"])

SpatialDE assumes a normally distributed noise. Since we just extracted raw counts, which empirically follow a negative binomial distribution, the counts data first needs to be transformed to a normal distributed noise. For this purpose SpatialDE uses a technique based on Anscombe:

norm_expr = NaiveDE.stabilize(counts.T).T

/home/icb/anna.schaar/miniconda3/envs/spatial-chapters/lib/python3.9/site-packages/scipy/optimize/_minpack_py.py:906: OptimizeWarning: Covariance of the parameters could not be estimated
  warnings.warn('Covariance of the parameters could not be estimated',

The transformed data still might include a varying library size across the spatial samples which can introduce a bias in the gene expression. SpatialDE recommends to account for this before actually performing the spatial test and regressing it out with the provided function:

resid_expr = NaiveDE.regress_out(total_counts, norm_expr.T, "np.log(total_counts)").T

We can now run the actual spatial test by passing the spatial coordinates and the normalized counts to SpatialDE. On the dataset, we are using here SpatialDE takes roughly 15 minutes when running it on all genes.

results = SpatialDE.run(adata.obsm["spatial"], resid_expr)

We can now inspect the result:

results.head()

	FSV	M	g	l	max_delta	max_ll	max_mu_hat	max_s2_t_hat	model	n	s2_FSV	s2_logdelta	time	BIC	max_ll_null	LLR	pval	qval
0	1.065401e-01	4	Mrpl15	68.5	8.383709e+00	-2836.151268	-8.553531	7.251817e+00	SE	2688	0.004038	3.928962e-01	0.009583	5703.888747	-2836.979729	0.828461	0.362718	0.462134
1	1.132153e-06	4	4732440D04Rik	68.5	8.830160e+05	1005.684545	-0.849110	8.478789e-07	SE	2688	0.043424	2.453021e+10	0.001693	-1979.782879	1005.684446	0.000099	0.992065	0.992308
2	2.556985e-01	4	Rrs1	68.5	2.910013e+00	-2372.430346	-5.025306	5.476694e+00	SE	2688	0.001739	5.062643e-02	0.003723	4776.446902	-2376.942619	4.512274	0.033652	0.056698
3	2.492298e-01	4	Cops5	68.5	3.011488e+00	-2579.842074	-11.139282	2.601672e+01	SE	2688	0.001748	5.234926e-02	0.003669	5191.270360	-2584.203162	4.361088	0.036769	0.061422
4	2.060557e-09	4	Cpa6	68.5	4.851652e+08	2817.673512	-0.768099	1.230862e-09	SE	2688	0.031727	5.410451e+15	0.001641	-5603.760814	2817.673419	0.000093	0.992305	0.992308

The resulting DataFrame contains the following important columns:

• g, the gene name

• l, a parameter indicating the genes distance scale a gene changes expression over

• pval, the p-value for spatial differential expression

• qval, the corrected p-value after correcting for multiple testing

We can now sort the result based on the corrected p-values (qval) and to better read the DataFrame, subset the table to only show g, l and qval. We will additionally save the object as top10 to conveniently use it for downstream plotting.

top10 = results.sort_values("qval").head(10)[["g", "l", "qval"]]
top10

	g	l	qval
7612	Esrra	443.950519	0.0
6586	Fbxo31	443.950519	0.0
6587	Jph3	443.950519	0.0
6588	Rpl13	443.950519	0.0
6589	Cpne7	443.950519	0.0
6590	Spata2l	443.950519	0.0
6591	Tcf25	443.950519	0.0
6592	Tubb3	443.950519	0.0
6593	Rhou	443.950519	0.0
6594	2810455O05Rik	443.950519	0.0

We can now plot the top-three significant genes and inspect their spatial pattern. We additionally plot the clusters of the dataset to analyze whether the detected genes might be linked to specific clusters.

sq.pl.spatial_scatter(adata, color=list(top10["g"][:3]) + ["cluster"])

As we can observe, all three genes show spatial patterns. Esrra does not seem to be associated with a specific cluster, but shows a spatial pattern in primarily the cortex layers, the thalamus and hypothalamus. Fbxo31 and Jph3 are primarily expressed in the pyramidal layer.

29.5. Key takeaways

• Spatially variable genes (SVGs) are genes that show a significant spatial pattern

• Methods designed for this task vary in complexity and model assumptions

• We recommend using multiple methods to identify SVGs and assess the result by plotting the gene’s expression in space.

29.6. References

[spatialAL21]

Alma Andersson and Joakim Lundeberg. Sepal: identifying transcript profiles with spatial patterns by diffusion-based modeling. Bioinformatics, 37(17):2644–2650, September 2021. URL: https://doi.org/10.1093/bioinformatics/btab164 (visited on 2023-07-03), doi:10.1093/bioinformatics/btab164.

[spatialHLC+21]

Jian Hu, Xiangjie Li, Kyle Coleman, Amelia Schroeder, Nan Ma, David J Irwin, Edward B Lee, Russell T Shinohara, and Mingyao Li. SpaGCN: integrating gene expression, spatial location and histology to identify spatial domains and spatially variable genes by graph convolutional network. Nat. Methods, 18(11):1342–1351, November 2021.

[spatialKVTS21]

Ilia Kats, Roser Vento-Tormo, and Oliver Stegle. SpatialDE2: Fast and localized variance component analysis of spatial transcriptomics. bioRxiv, pages 2021.10.27.466045, January 2021. URL: http://biorxiv.org/content/early/2021/11/11/2021.10.27.466045.abstract, doi:10.1101/2021.10.27.466045.

[spatialPSK+22]

Giovanni Palla, Hannah Spitzer, Michal Klein, David Fischer, Anna Christina Schaar, Louis Benedikt Kuemmerle, Sergei Rybakov, Ignacio L. Ibarra, Olle Holmberg, Isaac Virshup, Mohammad Lotfollahi, Sabrina Richter, and Fabian J. Theis. Squidpy: a scalable framework for spatial omics analysis. Nature Methods, 19(2):171–178, Feb 2022. URL: https://doi.org/10.1038/s41592-021-01358-2, doi:10.1038/s41592-021-01358-2.

[spatialSZZ20]

Shiquan Sun, Jiaqiang Zhu, and Xiang Zhou. Statistical analysis of spatial expression patterns for spatially resolved transcriptomic studies. Nature Methods, 17(2):193–200, February 2020. URL: https://doi.org/10.1038/s41592-019-0701-7, doi:10.1038/s41592-019-0701-7.

[spatialSTS18]

Valentine Svensson, Sarah A Teichmann, and Oliver Stegle. SpatialDE: identification of spatially variable genes. Nature Methods, 15(5):343–346, May 2018. URL: https://doi.org/10.1038/nmeth.4636, doi:10.1038/nmeth.4636.

[spatialWCR+22]

Benjamin L. Walker, Zixuan Cang, Honglei Ren, Eric Bourgain-Chang, and Qing Nie. Deciphering tissue structure and function using spatial transcriptomics. Communications Biology, 5(1):220, March 2022. URL: https://doi.org/10.1038/s42003-022-03175-5, doi:10.1038/s42003-022-03175-5.

[spatialZFW22]

Ke Zhang, Wanwan Feng, and Peng Wang. Identification of spatially variable genes with graph cuts. Nature Communications, 13(1):5488, September 2022. URL: https://doi.org/10.1038/s41467-022-33182-3, doi:10.1038/s41467-022-33182-3.

[spatialZSZ21]

Jiaqiang Zhu, Shiquan Sun, and Xiang Zhou. SPARK-X: non-parametric modeling enables scalable and robust detection of spatial expression patterns for large spatial transcriptomic studies. Genome Biology, 22(1):184, June 2021. URL: https://doi.org/10.1186/s13059-021-02404-0, doi:10.1186/s13059-021-02404-0.

29.7. Contributors

29.7.1. Authors

• Giovanni Palla

• Anna Schaar

29.7.2. Reviewers

• Lukas Heumos